Shor’s algorithm, named after mathematician Peter Shor, is the most commonly cited example of quantum algorithm. It solves the integer factorization problem in polynomial time, substantially faster than the most efficient known classical factoring algorithm, the general number field sieve, which works in sub-exponential time.
It owes its fame to its forecasted ability to break public-key cryptography schemes, which are based on the assumption that factoring large numbers is computationally infeasible. However, the greatest number so far factorized using Shor’s algorithm, 21, demonstrates how the technical difficulty of building a quantum computer is a limiting factor to real-life applications of quantum computing.
The different steps of Shor’s algorithm to factor an integer \(n\) are as follows:
- Pick \(a < n\) randomly using a uniform distribution.
- Calculate the greatest common divisor of \(a\) and \(n\) using Euclid’s algorithm. If \(\gcd(a, n) \neq 1\), this is a non-trivial factor of \(n\) and stop.
- Pick \(m\) such that \(m = 2^l\) for some integer \(l\) and \(n^2 \leq m < 2n^2\).
- Prepare two quantum registers in compound state \(\left|0\right\rangle \left|0\right\rangle\). Let them be large enough to represent numbers up to \(m-1\), i.e. of length \(l\).
- Apply the Hadamard transform to the first register.
The resulting state is \(\frac{1}{\sqrt{m}} \sum_{x=0}^{m-1} \left|x\right\rangle \left|0\right\rangle\). - Apply a map defined by \(\left|x\right\rangle \left|0\right\rangle \rightarrow \left|x\right\rangle \left|a^x \bmod n\right\rangle\).
This results in state \(\frac{1}{\sqrt{m}} \sum_{x=0}^{m-1} \left|x\right\rangle \left|a^x \bmod n\right\rangle\). - Apply the quantum Fourier transform to the first register, which becomes \(\frac{1}{\sqrt{m}} \sum_{y=0}^{m-1} e^\frac{2 \pi x y i}{m} \left|y\right\rangle\).
This results in global state \(\frac{1}{m} \sum_{x=0}^{m-1} \sum_{y=0}^{m-1}\) \(e^\frac{2 \pi x y i}{m} \left|y\right\rangle \left|a^x \bmod n\right\rangle\).
The goal here is to find the period \(p\) of \(x \rightarrow a^x \bmod n\). Let \(x = p q + r\) with \(r < p\) and \(q < \lfloor\frac{m – r}{p}\rfloor\). The state can be rewritten as the following: \(\frac{1}{m} \sum_{y=0}^{m-1} \sum_{r=0}^{p-1} \sum_{q=0}^{\lfloor\frac{m – r – 1}{p}\rfloor}\) \(e^\frac{2 \pi (p q + r) y i}{m} \left|y\right\rangle \left|a^r \bmod n\right\rangle\). - Observe the first register. The probability of observing a certain state \(\left|y\right\rangle \left|a^r \bmod n\right\rangle\) is \(\left| \frac{1}{m} \sum_{q=0}^{\lfloor\frac{m – r – 1}{p}\rfloor} e^\frac{2 \pi (p q + r) y i}{m} \right|^2\) \(= \frac{1}{m^2} \left| \sum_{q=0}^{\lfloor\frac{m – r – 1}{p}\rfloor} e^\frac{2 \pi p q y i}{m} \right|^2\).
Summing the geometric series gives \(\frac{1}{m^2} \left| \frac{1 – e^\frac{2 \pi p \lfloor\frac{m – r}{p}\rfloor y i}{m}}{1 – e^\frac{2 \pi p y i}{m}} \right|^2\) \(= \frac{1 – cos(\frac{2 \pi p \lfloor\frac{m – r}{p}\rfloor y}{m})}{m^2 (1 – cos(\frac{2 \pi p y}{m}))}\), which attains its maximal values when \(\frac{p y}{m}\) is the closest to an integer. Therefore, there is a high probability of observing \(y\) close to a multiple of \(\frac{m}{p}\) in the first register. - Perform continued fraction expansion on \(\frac{y}{m}\) to approximate it to \(\frac{k}{p’}\) with \(p’ < n\). The denominator \(p’\) is therefore likely to be the period \(p\) or a factor of it.
- Verify that \(a^{p’} \equiv 1 \bmod n\). If so, \(p = p’\): go to step 13.
- Otherwise, try the same thing with multiples of \(p’\). If it works, this gives \(p\): go to step 13.
- Otherwise, go back to step 4.
- If \(p\) is odd, go back to step 1.
- If \(a^{\frac{p}{2}} \equiv −1 \bmod n\), go back to step 1.
- Compute \(\gcd(a^{\frac{p}{2}} + 1, n)\) and \(\gcd(a^{\frac{p}{2}} – 1, n)\). They are both nontrivial factors of \(n\).
Now the process has been explained, we’ll start with the interface of our implementation. Our algorithm will be run in the following way:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
class Program { static void Main(string[] args) { int numberToFactor; do { Console.WriteLine("Enter a positive integer to factor:"); } while (!int.TryParse(Console.ReadLine(), out numberToFactor) || numberToFactor <= 0); ShorsAlgorithm shorsAlgorithm = new ShorsAlgorithm(new Random()); Console.WriteLine("Factors found for " + numberToFactor + ": " + string.Join(", ", shorsAlgorithm.Run(numberToFactor)) + "."); } } |
Note the use of dependency injection to avoid issues with pseudorandom number generator determinism.
The corresponding structure of the algorithm class will be as follows:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
class ShorsAlgorithm { protected Random Random; public ShorsAlgorithm(Random random) { this.Random = random; } public int[] Run(int numberToFactor) { // Run the algorithm } } |
Shor’s algorithm can be divided in two main sections: the classical part and the quantum period-finding subroutine. The implementation of the classical part is rather straightforward and can be done as follows:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
public int[] Run(int n) { // 1. Pick a < n randomly using a uniform distribution. int a = this.Random.Next(n); // 2. Calculate the greatest common divisor of a and n using Euclid’s algorithm. If gcd(a,n) ≠ 1, this is a non-trivial factor of n and stop. int greatestCommonDivisor = ShorsAlgorithm.GreatestCommonDivisor(a, n); if (greatestCommonDivisor != 1) { return new int[] { greatestCommonDivisor }; } // 3. to 12. Find the period of x → a^x mod n. int period = this.Period(n, a); // 13. If p is odd, go back to step 1. if (period % 2 == 1) { return this.Run(n); } // 14. If a^(p/2) ≡ −1 mod n, go back to step 1. int power = ShorsAlgorithm.IntPow(a, period / 2); if (power % n == n - 1) { return this.Run(n); } // 15. Compute gcd(a^(p/2) + 1, n) and gcd(a^(p/2) – 1, n). They are both nontrivial factors of n. return new int[] { ShorsAlgorithm.GreatestCommonDivisor(power + 1, n), ShorsAlgorithm.GreatestCommonDivisor(power - 1, n) }; } |
The greatest common divisor is calculated recursively using Euclid’s algorithm:
|
1 2 3 4 |
protected static int GreatestCommonDivisor(int a, int b) { return b == 0 ? a : ShorsAlgorithm.GreatestCommonDivisor(b, a % b); } |
And we use exponentiation by squaring to calculate integer powers:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
protected static int IntPow(int @base, int exponent) { int result = 1; while (exponent > 0) { if ((exponent & 1) == 1) { result *= @base; } exponent >>= 1; @base *= @base; } return result; } |
Exponentiation by squaring uses the fact that \(x^n= x (x^{2})^{\frac{n – 1}{2}}\) if \(n\) is odd and \((x^{2})^{\frac{n}{2}}\) if \(n\) is even, allowing powers to be calculated using multiplication only. A quick benchmark shows, without much surprise, that this approach is more than three times as fast as using .NET’s native double Math.Pow(double, double) implementation and casting it to an int.
Next is the period-finding subroutine, the quantum part of Shor’s algorithm. We will use Quantum.NET to simulate the required quantum circuit, shown below:
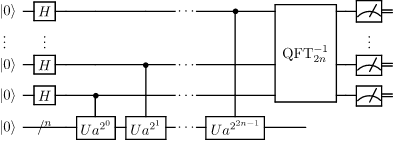
Initializing the input and output quantum registers is as simple as it gets:
|
1 2 3 4 5 6 |
// 3. Pick m such that m = 2^l for some integer l and n² ≤ m < 2n². int registerLength = ShorsAlgorithm.RegisterLength(n * n - 1); // 4. Prepare two quantum registers in compound state |0⟩|0⟩. Let them be large enough to represent numbers up to m − 1, i.e. of length l. QuantumRegister inputRegister = new QuantumRegister(0, registerLength); QuantumRegister outputRegister = new QuantumRegister(0, registerLength); |
And so is applying the Hadamard transform to the first register:
|
1 2 |
// 5. Apply the Hadamard transform to the first register. inputRegister = QuantumGate.HadamardGateOfLength(registerLength) * inputRegister; |
We use the following method to calculate \(m\):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
protected static int RegisterLength(int value) { int length = 1; for (int bitCount = 16; bitCount > 0; bitCount /= 2) { if (value >= 1 << bitCount) { value >>= bitCount; length += bitCount; } } return length; } |
Another quick benchmark shows it to be about 3.6 times as fast as the equivalent approach using .NET’s logarithm, (int) Math.Log(n * n - 1, 2) + 1. It works by removing chunks of 16, 8, 4, 2 and 1 bit(s) (we’re working on 32-bit integers) when possible and counting the number of bits removed.
Now to the crux of Shor’s algorithm, but also the bottleneck in terms of runtime: modular exponentiation. We have to build a gate (more like a sub-circuit) that applies the map defined by \(\left|x\right\rangle \left|0\right\rangle \rightarrow \left|x\right\rangle \left|a^x \bmod n\right\rangle\) to the full register.
Building such a circuit is a very complex matter and there are many approaches, but all start with a decomposition into modular multipliers. We use the fact that \(a^x \bmod n\) \(= \prod_{i=0}^{l-1} (a^{2^{i}} \bmod n)^{x_i} \bmod n\), where the \(x_i\) are the bits of \(x\) such that \(x = \sum_{i=0}^{l-1} x_i 2^i\), to split the circuit into a series of controlled modular multiplication gates, each using a different qubit from the input register as a control qubit.
However, for the sake of simplicity, we will represent this circuit with a unique modular exponentiation gate. The map leaves the input registry unchanged, therefore it can be represented by a block diagonal matrix of total order \(m^2\):
\mathbf{M}_{0} & 0 & \cdots & 0 \\ 0 & \mathbf{M}_{1} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & \mathbf{M}_{m – 1}
\end{bmatrix}\)
It also overrides the output registry regardless of its initial value (with the result of the modular exponentiation of the input registry), therefore the elements of \(\mathbf{M}_{k}\) are \(\mathbf{{m}_{k}}_{i, j} = 1\) if \(i = a^k \bmod n\) and \(0\) otherwise, regardless of \(j\).
The resulting permutation matrix is built using the following:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
protected static Matrix<Complex> ModularExponentiationMatrix(int n, int a, int registerLength) { int matrixSize = 1 << (registerLength * 2); Matrix<Complex> modularExponentiationMatrix = Matrix<Complex>.Build.Sparse(matrixSize, matrixSize); int blockSize = 1 << registerLength; for (int i = 0; i < blockSize; i++) { int modularExponentiationResult = ShorsAlgorithm.ModIntPow(a, i, n); for (int j = 0; j < blockSize; j++) { modularExponentiationMatrix.At(i * blockSize + modularExponentiationResult, i * blockSize + j, 1); } } return modularExponentiationMatrix; } |
Modular exponentiation is performed using a slightly modified version of exponentiation by squaring:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
protected static int ModIntPow(int @base, int exponent, int modulus) { int result = 1; while (exponent > 0) { if ((exponent & 1) == 1) { result = (result * @base) % modulus; } exponent >>= 1; @base = (@base * @base) % modulus; } return result; } |
We use the newly created permutation matrix to create a quantum gate we apply to the global register, formed from the input and output registers.
|
1 2 3 4 5 6 7 |
// 6. Apply a map defined by |x⟩ |0⟩ → |x⟩ |a^x mod n⟩. Matrix<Complex> modularExponentiationMatrix = ShorsAlgorithm.ModularExponentiationMatrix(n, a, registerLength); QuantumGate modularExponentiationGate = new QuantumGate(modularExponentiationMatrix); QuantumRegister fullRegister = new QuantumRegister(inputRegister, outputRegister); fullRegister = modularExponentiationGate * fullRegister; |
The registers are now entangled. The next step consists in applying the quantum Fourier transform to the input register, but it needs to be processed along with the output register in order to preserve entanglement. The solution consists in creating a quantum gate from two smaller ones: a quantum Fourier transform for the input register and an identity gate for the output register, which will be left unchanged.
|
1 2 3 4 |
// 7. Apply the quantum Fourier transform to the first register, which becomes 1/√m ∑(y=0...m−1) e^(2πxyi/m) |y⟩. QuantumGate quantumFourierMatrixPlusIdentity = new QuantumGate(QuantumGate.QuantumFourierTransform(registerLength), QuantumGate.IdentityGateOfLength(registerLength)); fullRegister = quantumFourierMatrixPlusIdentity * fullRegister; |
It is now time to observe the first register so that it collapses into a pure state, and read its value. fullRegister is of length 2 * registerLength, so we use the portionStart and portionLength parameters of QuantumRegister.GetValue to only read the first registerLength bits, returning a value \(y\):
|
1 2 3 4 |
// 8. Observe the first register. fullRegister.Collapse(this.Random); int inputRegisterValue = fullRegister.GetValue(0, registerLength); |
The idea is now to perform continued fraction expansion on \(y / m\). As explained above, the denominator of the fraction approximation is likely to be the period \(p\) or a factor of it.
|
1 2 3 4 |
// 9. Perform continued fraction expansion on y/m to approximate it to k/p′ with p′ < n. The denominator p′ is therefore likely to be the period p or a factor of it. float ratio = (float) inputRegisterValue / (1 << registerLength); int denominator = ShorsAlgorithm.Denominator(ratio, n); |
Every irrational number can be represented in precisely one way as an infinite continued fraction, which is an expression of the form:
Limiting the expression to a certain number of terms gives rational approximations called the convergents of the continued fraction. They are \(a_0 = \frac{a_0}{1}\), \(a_0 + \frac{1}{a_1} = \frac{a_1 a_0 + 1}{a_1 }\), \(a_0 + \frac{1}{a_1 + \frac{1}{a_2}} = \frac{a_2 (a_1 a_0 + 1) + a_0}{a_2 a_1 + 1}\), and can generally be expressed as \(\frac{h_n}{k_n}\), with the numerators and denominators recursively defined by \(h_n = a_n h_{n − 1} + h_{n − 2}\) and \(k_n = a_n k_{n − 1} + k_{n − 2}\).
This property allows us to find the greatest denominator \(p’\) such that\(p’ < n\), using the following implementation:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
protected static int Denominator(float realNumber, int maximum) { if (realNumber == 0f) { return 1; } int coefficient = 0; float remainder = realNumber; int[] previousNumerators = new int[] { 0, 1 }; int[] previousDenominators = new int[] { 1, 0 }; while (remainder != Math.Floor(remainder)) { coefficient = (int) remainder; try { remainder = checked(1f / (remainder - coefficient)); } catch (System.OverflowException) { return previousDenominators[1]; } int numerator = coefficient * previousNumerators[1] + previousNumerators[0]; int denominator = coefficient * previousDenominators[1] + previousDenominators[0]; if (denominator >= maximum) { return previousDenominators[1]; } previousNumerators[0] = previousNumerators[1]; previousDenominators[0] = previousDenominators[1]; previousNumerators[1] = numerator; previousDenominators[1] = denominator; } return previousDenominators[1]; } |
Now we have a candidate for \(p\), we verify if \(p’\) or one of its multiples is the period we’re looking for.
|
1 2 3 4 5 6 7 8 9 |
// 10. and 11. Verify that a^p′ ≡ 1 mod n. Otherwise, try the same thing with multiples of p′. for (int period = denominator; period < n; period += denominator) { //if (ShorsAlgorithm.IntPow(a, period) % n == 1) if (ShorsAlgorithm.ModIntPow(a, period, n) == 1) { return period; } } |
If that’s the case, then we are done with the period-finding subroutine, and Shor’s algorithm as a whole. If not, we start the subroutine over:
|
1 2 |
// 12. Otherwise, go back to step 4. return this.Period(n, a); |
This article now comes to an end. We have successfully modeled Shor’s algorithm, and while it won’t help us factor anything (the classical alternatives being incomparably faster than simulating a system whose complexity grows exponentially with regard to the size of the input), it provides us with great insight as to how the algorithm can be implemented in practice.
RSA is not broken yet.